Additional Statistics Examples

1 Sample Quantile-Quantile(Q-Q) plot

qqplot is a visual method that detemines how close a distribution to be a normal distribution.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from statsmodels.api import qqplot

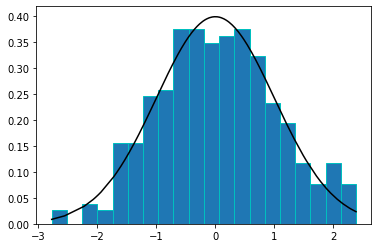
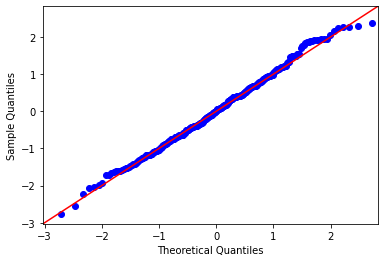
Normally distributed data

from scipy.stats import norm
data = norm.rvs(random_state=0, size=(300,))
data.sort()

plt.hist(data, bins=20, density=True, edgecolor='c')
plt.plot(data, norm.pdf(data), 'k')
qqplot(data=data, line='45')
plt.show()

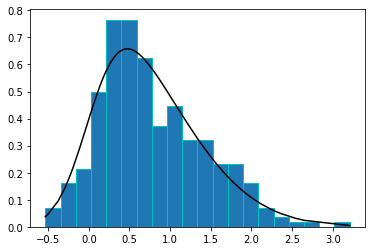
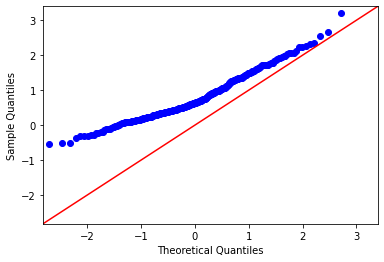
Right skewed data

from scipy.stats import skewnorm

skewness = 3

data = skewnorm.rvs(a = skewness, random_state=0, size=(300,))
data.sort()

plt.hist(data, bins=20, density=True, edgecolor='c')
plt.plot(data, skewnorm.pdf(data, a=skewness), 'k')
qqplot(data=data, line='45')
plt.show()

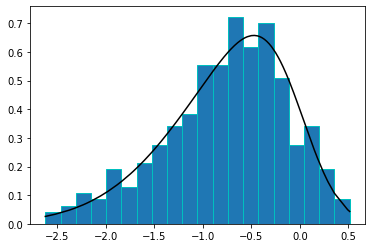
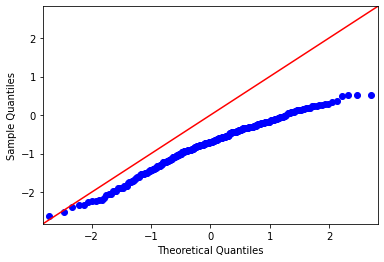
Left skewed data

from scipy.stats import skewnorm

skewness = -3

data = skewnorm.rvs(a = skewness, random_state=0, size=(300,))
data.sort()

plt.hist(data, bins=20, density=True, edgecolor='c')
plt.plot(data, skewnorm.pdf(data, a=skewness), 'k')
qqplot(data=data, line='45')
plt.show()

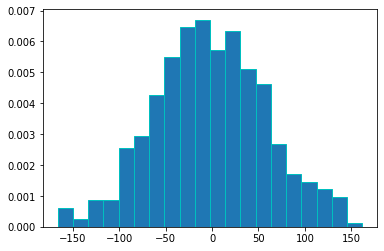
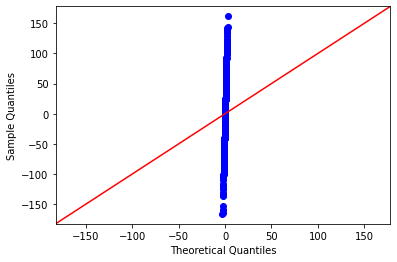
Flat data

from scipy.stats import kurtosis

data = norm.rvs(scale=60, random_state=0, size=(500,))
print("kurtosis :",kurtosis(data))

plt.hist(data, bins=20, density=True, edgecolor='c')
qqplot(data=data, line='45')
plt.show()

kurtosis : -0.13960668644127638

2 Samples Quantile-Quantile(Q-Q) plot

from statsmodels.api import qqplot_2samples

from scipy.stats import norm
data = norm.rvs(random_state=0, size=(150,2))

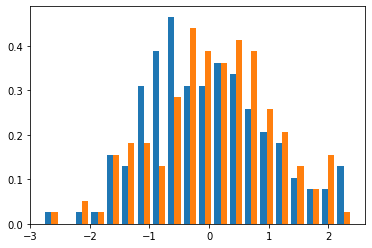
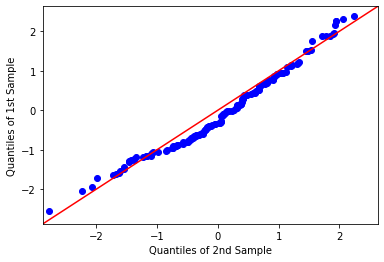
plt.hist(data, density=True, bins=20)
qqplot_2samples(data[:,0], data[:,1],line='45')
plt.show()