Denoising data using Fast Fourier#
[1]:
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import style
from mightypy.make import sine_wave_from_sample, sine_wave_from_timesteps
style.use("seaborn")
%matplotlib inline
Genereting a noisy signal#
[13]:
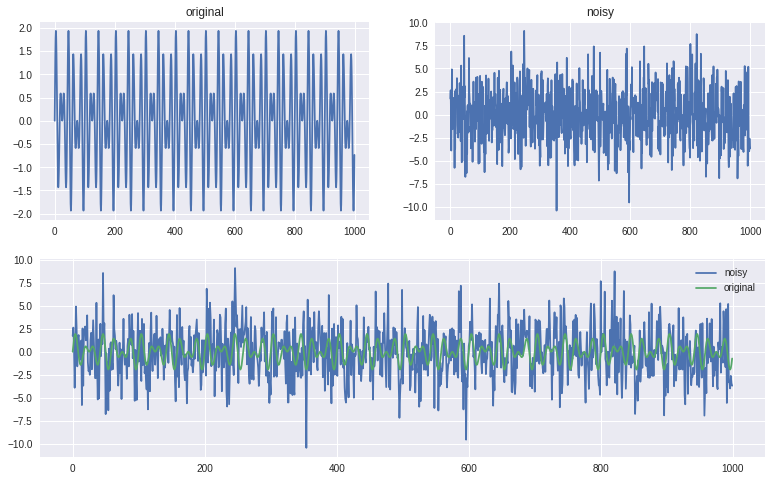
time_step = 0.001
wave1, time1, freqs1 = sine_wave_from_timesteps(signal_freq=50,time_step=time_step)
wave2, time2, freqs2 = sine_wave_from_timesteps(signal_freq=70,time_step=time_step)
original_signal = wave1 + wave2
N = len(original_signal)
noisy_signal = original_signal + 2.5 * np.random.randn(N) # adding random noise here
fig = plt.figure(figsize=(13,8))
ax1 = fig.add_subplot(2,2,1)
ax2 = fig.add_subplot(2,2,2)
ax3 = fig.add_subplot(2,2,(3,4))
ax1.plot(original_signal)
ax1.set_title("original")
ax2.plot(noisy_signal)
ax2.set_title("noisy")
ax3.plot(noisy_signal,label="noisy")
ax3.plot(original_signal, label="original")
plt.legend()
[13]:
<matplotlib.legend.Legend at 0x7f64984328b0>
Calculating FFT#
[3]:
f_hat = np.fft.fft(noisy_signal,N)
[4]:
n = int(np.floor(N/2)) # frequencies till N/2 can be used for this processing
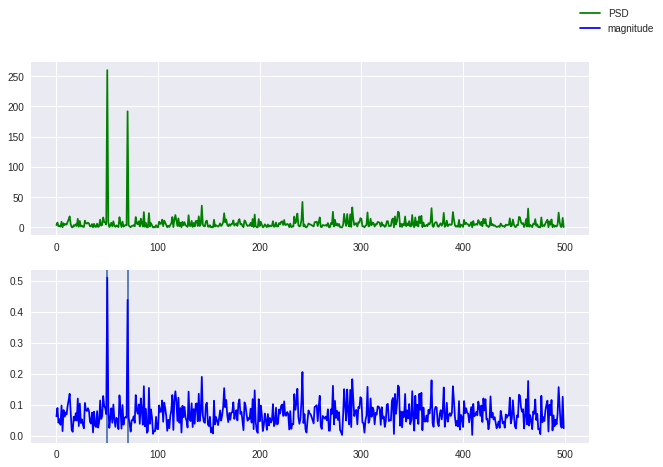
Power Spectral Density#
power spectral density is measure of signal power.
how the strength of a signal is distributed in the frequency domain.
\(\lambda = a + ib\\ \overline{\lambda} = a - ib\)
\(\lambda . \overline{\lambda} = \lambda^2 = a^2 + b^2\)
[5]:
new_freqs = (1/(N*time_step)) * np.arange(N)
[6]:
psd = (f_hat * np.conjugate(f_hat) / N).real # imag is already 0
mag = (np.abs(f_hat) / N).real # imag is already 0
[7]:
fig,ax = plt.subplots(2,1,figsize=(10,7))
plt.axvline(50)
plt.axvline(70)
ax[0].plot(new_freqs[:n],psd[:n],'g',label='PSD')
ax[1].plot(new_freqs[:n],mag[:n],'b',label="magnitude")
fig.legend()
[7]:
<matplotlib.legend.Legend at 0x7f6498896f40>
Pickup index based on PSD threshold#
it will give True value for idxs to keep and False value for idxs to make 0
[8]:
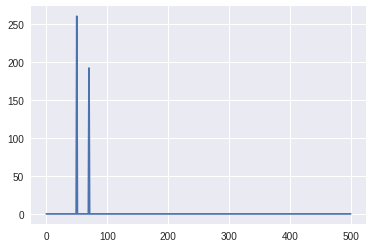
threshold_idxs = (psd > 100)
Cleanup using PSD#
multiply it with the psd signal to cleanup noisy enery signals
[9]:
cleaned_psd = psd * threshold_idxs
plt.plot(new_freqs[:n],cleaned_psd[:n])
[9]:
[<matplotlib.lines.Line2D at 0x7f649882eaf0>]
Cleanup frequency transforms#
similarly multiply it with the f_hat to cleanup frequecies
[10]:
cleaned_f_hat = f_hat * threshold_idxs
Regenerate signal using Inverse Fourier Transform#
[11]:
regen_signal = np.fft.ifft(cleaned_f_hat).real
[12]:
fig,ax = plt.subplots(3,1,figsize=(15,15))
ax[0].plot(noisy_signal,label="noisy signal")
ax[0].plot(original_signal,label="original signal")
ax[0].legend()
ax[1].plot(noisy_signal,label="noisy signal")
ax[1].plot(regen_signal,label="recovered signal")
ax[1].legend()
ax[2].plot(original_signal,label="original signal")
ax[2].plot(regen_signal,label="recovered signal")
ax[2].legend()
plt.show()

