Distance Metrics#
[6]:
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import style
style.use('seaborn')
%matplotlib inline
[7]:
m = np.array([
[2, 0],
[0, 2],
[4, -1]
])
[15]:
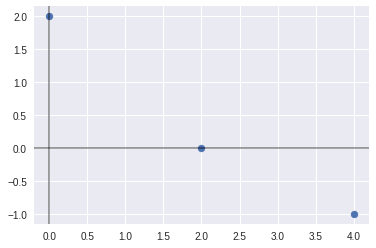
x,y = m[:,[0]],m[:,[1]]
plt.axhline(alpha=0.4, c='k')
plt.axvline(alpha=0.4, c='k')
plt.scatter(x,y)
plt.show()
[16]:
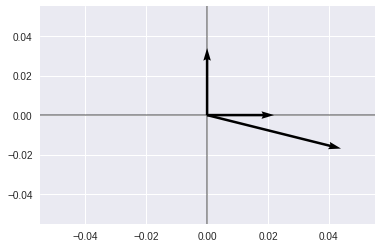
x,y = m[:,[0]],m[:,[1]]
plt.axhline(alpha=0.4, c='k')
plt.axvline(alpha=0.4, c='k')
plt.quiver(*np.zeros_like(m.T),x,y,scale=10)
plt.show()
Minkowski distance#
\(d = (\sum_{i=1}^{n} \bigl| {||x||}_r - {||z||}_r \bigr|^p)^{\frac{1}{p}}\)
p |
distance metric |
|---|---|
p = 1 |
manhattan |
p = 2 |
Euclidean |
\[p \rightarrow \infty\]
|
max |
[17]:
from scipy.spatial import minkowski_distance
[24]:
m[0], m[1]
[24]:
(array([2, 0]), array([0, 2]))
[20]:
minkowski_distance(m[0], m[1], p=1)
[20]:
4.0
[21]:
minkowski_distance(m[0], m[1], p=2)
[21]:
2.8284271247461903
[23]:
minkowski_distance(m[0], m[1], p=np.inf)
[23]:
2.0
Manhattan distance#
\(\vec{v_1} = [x_1,y_1]\)
\(\vec{v_2} = [x_2,y_2]\)
\(d = |{x_2} - {x_1}| + |{y_2} - {y_1}|\)
complete distance between two points considering the path is not linear
like going from one building to another
[14]:
from sklearn.metrics.pairwise import manhattan_distances
[73]:
m, manhattan_distances(m)
[73]:
(array([[ 2, 0],
[ 0, 2],
[ 4, -1]]),
array([[0., 4., 3.],
[4., 0., 7.],
[3., 7., 0.]]))
[74]:
def manhattan_distances_scratch(v1,v2):
return np.abs(v2 - v1).sum()
[75]:
manhattan_distances_scratch(m[0],m[1])
[75]:
4
[76]:
manhattan_distances_scratch(m[0],m[2])
[76]:
3
[78]:
manhattan_distances_scratch(m[1],m[2])
[78]:
7
Euclidean distance#
\(\vec{v_1} = [x_1,y_1]\)
\(\vec{v_2} = [x_2,y_2]\)
\(d = \sqrt{({\vec{v_2} - \vec{v_1}})^2}\)
\(d = \sqrt{({x_2} - {x_1})^2 + ({y_2} - {y_1})^2}\)
direct distance between two points
like flying from one city to another
[8]:
from sklearn.metrics.pairwise import euclidean_distances
[66]:
m,euclidean_distances(m)
[66]:
(array([[ 2, 0],
[ 0, 2],
[ 4, -1]]),
array([[0. , 2.82842712, 2.23606798],
[2.82842712, 0. , 5. ],
[2.23606798, 5. , 0. ]]))
[59]:
m[0], m[1]
[59]:
(array([2, 0]), array([0, 2]))
[69]:
def euclidean_distances_scratch(v1,v2):
return np.sqrt(np.square(v2 - v1).sum())
[70]:
euclidean_distances_scratch(m[0],m[1])
[70]:
2.8284271247461903
[71]:
euclidean_distances_scratch(m[0],m[2])
[71]:
2.23606797749979
[72]:
euclidean_distances_scratch(m[1],m[2])
[72]:
5.0
Cosine distance & Cosine Similarity#
\(\vec{A}.\vec{B} = ||\vec{A}|| * ||\vec{B}|| * cos(\theta)\)
\(\theta\) = Angle between \(\vec{A}\) and \(\vec{B}\)
Cosine distance = \(cosine(A,B) = \frac{\vec{A}.\vec{B}}{||\vec{A}|| * ||\vec{B}||} = \frac{\sum{A_i . B_i}}{\sqrt{\sum{A_i^2}}\sqrt{\sum{B_i^2}}}\)
cosine similarity = 1 - cosine distance
angular distance between two points
[5]:
from sklearn.metrics.pairwise import cosine_similarity
[6]:
m,cosine_similarity(m)
[6]:
(array([[ 2, 0],
[ 0, 2],
[ 4, -1]]),
array([[ 1. , 0. , 0.9701425 ],
[ 0. , 1. , -0.24253563],
[ 0.9701425 , -0.24253563, 1. ]]))
[42]:
def cosine_similarity_scratch(v1,v2):
return (v1 * v2).sum() / (np.linalg.norm(v1) * np.linalg.norm(v2))
[45]:
cosine_similarity_scratch(m[0],m[1])
[45]:
0.0
[43]:
cosine_similarity_scratch(m[0],m[2])
[43]:
0.9701425001453319
[47]:
cosine_similarity_scratch(m[1],m[2])
[47]:
-0.24253562503633297
