Classification Evaluation Metrics#
Here we are specifically talking about binary classification. but the concepts mentioned are applicable to multiclass classification also.
References#
https://en.wikipedia.org/wiki/Evaluation_of_binary_classifiers
https://scikit-learn.org/stable/modules/generated/sklearn.metrics.confusion_matrix.html
https://scikit-learn.org/stable/auto_examples/model_selection/plot_precision_recall.html
https://developers.google.com/machine-learning/crash-course/classification/roc-and-auc
[1]:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.metrics import (accuracy_score, precision_score, recall_score,
precision_recall_curve, roc_auc_score, roc_curve,
RocCurveDisplay, ConfusionMatrixDisplay, confusion_matrix,
f1_score, PrecisionRecallDisplay, auc, classification_report)
Conditions#
Positive |
Negative |
|---|---|
The number of real positive cases in the data. |
The number of real negative cases in the data. |
Confusion Matrix#
Sometimes referred as error matrix, it allows us to visualize performance of the machine learning. it is a matrix that shows comparison between actual values and predicted values.
One general understanding for confusion matrix
Predicted Values
+--------------------+--------------------+
| Positive | Negative |
+----------+--------------------+--------------------+
Actual | Positive | True Positive(TP) | False Negative(FN) |
+----------+--------------------+--------------------+
Values | Negative | False Positive(FP) | True Negative(TN) |
+----------+--------------------+--------------------+

[12]:
y_true = np.array([1, 0, 0, 1, 0, 1, 0, 1, 1, 0])
y_pred = np.array([1, 0, 1, 1, 0, 0, 0, 1, 1, 1])
confusion_mat = confusion_matrix(y_true, y_pred)
confusion_mat
[12]:
array([[3, 2],
[1, 4]])
understandably 3 correct 0s, 4 correct 1s and then the wrong ones. 2 false 1s and 1 false 0.
[13]:
ConfusionMatrixDisplay(confusion_mat).plot()
plt.show()
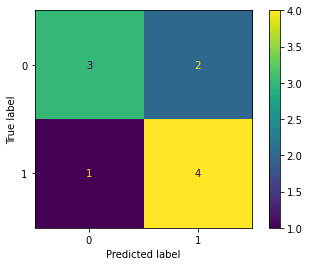
When we are talking about TP, FP, FN, FP these are relative terms/ conditions in the sense of labels. when we are talking about label 1 then the matrix above looks like this
0 1
+------+------+
0 | TN | FP |
+------+------+
1 | FN | TP |
+------+------+
[14]:
tn1, fp1, fn1, tp1 = confusion_mat.ravel()
tn1, fp1, fn1, tp1
[14]:
(3, 2, 1, 4)
or if we are talking about label 0 then
0 1
+------+------+
0 | TP | FN |
+------+------+
1 | FP | TN |
+------+------+
[15]:
tp0, fn0, fp0, tn0 = confusion_mat.ravel()
tp0, fn0, fp0, tn0
[15]:
(3, 2, 1, 4)
Errors#
Type 1 Error/ False Positive (FP) |
Type 2 Error/ False Negative (FN) |
|---|---|
Mistakenly concluding results as true (having an affect), but they are actually not (due to random chance). |
Mistakenly concluding results as false (due to random chance), but they actually have an affect of hypothesis. |
Accuracy#
As the name suggests how accurate the predicted results are.
\begin{align} \text{accuracy} &= \frac{TP + TN}{TP + FP + TN + FN} = \frac{\text{correct results count}}{\text{total count}} \end{align}
accuracy is not dependent on label.
[16]:
y_true, y_pred
[16]:
(array([1, 0, 0, 1, 0, 1, 0, 1, 1, 0]), array([1, 0, 1, 1, 0, 0, 0, 1, 1, 1]))
[17]:
accuracy_score(y_true, y_pred)
[17]:
0.7
[18]:
(tp0 + tn0) / (tp0 + fp0 + tn0 + fn0)
[18]:
0.7
[19]:
(tp1 + tn1) / (tp1 + fp1 + tn1 + fn1)
[19]:
0.7
Precision#
it shows how precise we are in our results.
by definition in all the predicted values, how many of them actually have correct values.
\begin{align} \text{precision} = \frac{TP}{TP + FP} = \frac{TP}{\text{predicted positives}} \end{align}
[30]:
y_true, y_pred
[30]:
(array([1, 0, 0, 1, 0, 1, 0, 1, 1, 0]), array([1, 0, 1, 1, 0, 0, 0, 1, 1, 1]))
[20]:
precision_score(y_true, y_pred, pos_label=1)
[20]:
0.6666666666666666
[21]:
tp1 / (tp1 + fp1)
[21]:
0.6666666666666666
[22]:
precision_score(y_true, y_pred, pos_label=0)
[22]:
0.75
[23]:
tp0 / (tp0 + fp0)
[23]:
0.75
Recall / Sensitivity / True Positive Rate (TPR) / Hit Rate#
it shows how many of the correct values we can recall.
by definition how many correct values the model can recall.
refers to the probability of a positive test, conditioned on truly being positive.
\begin{align} recall = \frac{TP}{TP + FN} = \frac{TP}{\text{actual positives}} \end{align}
[31]:
y_true, y_pred
[31]:
(array([1, 0, 0, 1, 0, 1, 0, 1, 1, 0]), array([1, 0, 1, 1, 0, 0, 0, 1, 1, 1]))
[32]:
recall_score(y_true, y_pred, pos_label=1)W
[32]:
0.8
[33]:
tp1 / (tp1 + fn1)
[33]:
0.8
[34]:
recall_score(y_true, y_pred, pos_label=0)
[34]:
0.6
[35]:
tp0 / (tp0 + fn0)
[35]:
0.6
F1-score#
The F1-score combines the precision and recall of a classifier into a single metric by taking their harmonic mean. It is primarily used to compare the performance of two classifiers. Suppose that classifier A has a higher recall, and classifier B has higher precision.
\begin{align} F1 &= \frac{2}{\frac{1}{\text{Precision}} + \frac{1}{\text{Recall}}}\\ F1 &= \frac{2 \times \text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}}\\ F1 &= \frac{2 \times TP}{(2 \times TP) + FP + FN} \end{align}
[36]:
y_true, y_pred
[36]:
(array([1, 0, 0, 1, 0, 1, 0, 1, 1, 0]), array([1, 0, 1, 1, 0, 0, 0, 1, 1, 1]))
[37]:
f1_score(y_true, y_pred, pos_label=1)
[37]:
0.7272727272727272
[38]:
f1_score(y_true, y_pred, pos_label=0)
[38]:
0.6666666666666665
Classification Report#
Novelty from Scikit-Learn
[39]:
print(classification_report(y_true, y_pred))
precision recall f1-score support
0 0.75 0.60 0.67 5
1 0.67 0.80 0.73 5
accuracy 0.70 10
macro avg 0.71 0.70 0.70 10
weighted avg 0.71 0.70 0.70 10
Specificity / Selectvity / True Negative Rate (TNR)#
refers to the probability of a negative test, conditioned on truly being negative.
\begin{align} \text{specificity} &= \frac{TN}{TN + FP} \end{align}
[40]:
tn0 / (tn0 + fp0)
[40]:
0.8
[41]:
tn1 / (tn1 + fp1)
[41]:
0.6
Fall Out / False Positive Rate (FPR)/ False Alarm#
The false positive rate is calculated as the ratio between the number of negative events wrongly categorized as positive (false positives) and the total number of actual negative events (regardless of classification).
The false positive rate (or “false alarm rate”) usually refers to the expectancy of the false positive ratio.
\begin{align} FPR = \frac{FP}{FP + TN} \end{align}
[42]:
fp0 / (fp0 + tn0)
[42]:
0.2
[43]:
fp1 / (fp1 + tn1)
[43]:
0.4
Miss rate / False Negative Rate (FNR)#
\begin{align} FNR = \frac{FN}{FN + TP} \end{align}
[44]:
fn0 / (fn0 + tp0)
[44]:
0.4
[45]:
fn1 / (fn1 + tp1)
[45]:
0.2
PRC (Precision-Recall Curve)#
The precision-recall curve shows the tradeoff between precision and recall for different threshold. A high area under the curve represents both high recall and high precision, where high precision relates to a low false positive rate, and high recall relates to a low false negative rate.
[46]:
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
mat_x, mat_y = make_classification(n_samples=1000)
mat_x.shape, mat_y.shape
estimator = LogisticRegression()
estimator.fit(mat_x, mat_y)
pred_y = estimator.predict(mat_x)
[47]:
fig, ax = plt.subplots(1, 2, figsize=(10,5))
PrecisionRecallDisplay.from_predictions(mat_y, pred_y, name='logistic regression', pos_label=1, ax=ax[0])
PrecisionRecallDisplay.from_predictions(mat_y, pred_y, name='logistic regression', pos_label=0, ax=ax[1])
plt.show()
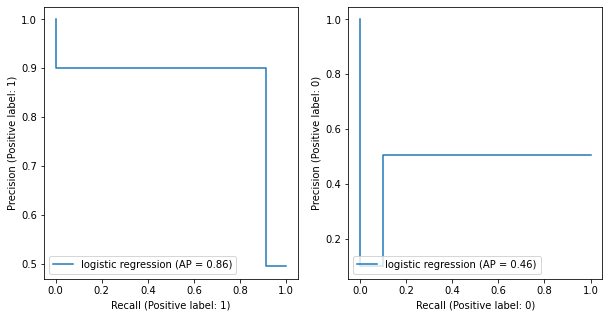
[48]:
fig, ax = plt.subplots(1, 2, figsize=(10,5))
PrecisionRecallDisplay.from_estimator(estimator, mat_x, mat_y, pos_label=1, ax=ax[0])
PrecisionRecallDisplay.from_estimator(estimator, mat_x, mat_y, pos_label=0, ax=ax[1])
plt.legend(loc='best')
plt.show()
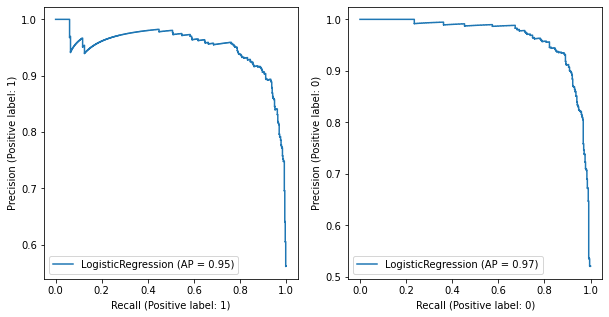
[49]:
precision, recall, threshold = precision_recall_curve(y_true=mat_y, probas_pred=pred_y,
pos_label=1)
auc(recall, precision)
[49]:
0.9276553559547571
[50]:
precision, recall, threshold = precision_recall_curve(y_true=mat_y, probas_pred=pred_y,
pos_label=0)
auc(recall, precision)
[50]:
0.3269051500958479
ROC (Receiver Operating Characteristic Curve)#
An ROC curve (receiver operating characteristic curve) is a graph showing the performance of a classification model at all classification thresholds. This curve plots two parameters: True Positive Rate. False Positive Rate.
[51]:
fig, ax = plt.subplots(1, 2, figsize=(10,5))
RocCurveDisplay.from_estimator(estimator, mat_x, mat_y, pos_label=1, ax=ax[0])
RocCurveDisplay.from_estimator(estimator, mat_x, mat_y, pos_label=1, ax=ax[1])
plt.legend(loc='best')
plt.show()
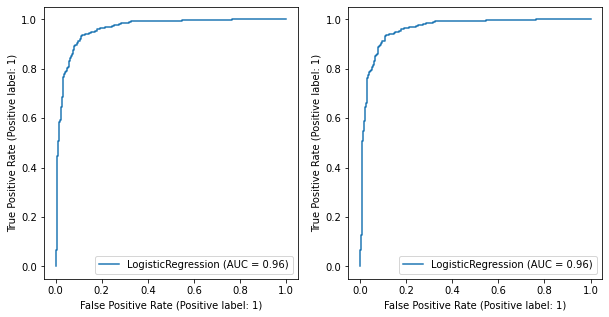
[52]:
roc_auc_score(mat_y, pred_y)
[52]:
0.906050605060506
