Loss Functions

References

• https://en.wikipedia.org/wiki/Loss_functions_for_classification

• https://en.wikipedia.org/wiki/Hinge_loss

• https://www.cs.cornell.edu/courses/cs4780/2018fa/lectures/lecturenote10.html

import numpy as np
from sklearn import metrics

import matplotlib.pyplot as plt

plt.style.use("fivethirtyeight")

Loss vs Cost Function

\begin{align} \text{Cost Function } J(h_w(X), y) = \frac{1}{N} \sum_{i=1}^{N} L(h_w(x_i), y_i) \end{align}

Classification Loss

Hinge Loss

\begin{align} L(h_w(x_i), y_i) = \max(1 - h_w(x_i) y_i, 0)^p \end{align}

p	Usecase
p = 1	SVM
p = 2	Squared Loss SVM

• Generally used for Standard SVM

def hinge_loss(y_true, y_pred, p):
    return np.power(np.max(np.c_[1 - (y_true * y_pred), np.zeros_like(y_true)], axis=1), p)

Correct classification

hinge_loss(-1, -1, 1), hinge_loss(-1, -1, 2)

(array([0]), array([0]))

Incorrect Classification

hinge_loss(-1, 1, 1), hinge_loss(1, -1, 1)

(array([2]), array([2]))

y_true = np.array([1, -1, 1, -1, 1, -1, 1, -1, 1])
y_pred = np.array([-1, -1, 1, -1, 1, -1, -1, -1, 1])

metrics.hinge_loss(y_pred, y_true), hinge_loss(y_true, y_pred, 1).mean()

(0.4444444444444444, 0.4444444444444444)

metrics.hinge_loss([-1], [-1]), metrics.hinge_loss([-1], [1])

(0.0, 2.0)

Log Loss

\begin{align} L(h_w(x_i), y_i) = \log(1 + e^{- y_i h_w(x_i)}) \end{align}

• Used for Logistic Regression

def logistic_loss(y_true, y_pred):
    return np.log(1 + np.exp(-(y_true * y_pred)))

def log_loss(y_true, y_pred):
    return ((y_true * np.log(y_pred)) + ((1 - y_true) * np.log(1 - y_pred)))

Correct classification

logistic_loss(-1, -1), logistic_loss(1, 1)

(0.31326168751822286, 0.31326168751822286)

Incorrect Classification

logistic_loss(-1, 1), logistic_loss(1, -1)

(1.3132616875182228, 1.3132616875182228)

y_true = np.array([1, -1, 1, -1, 1, -1, 1, -1, 1])
y_pred = np.array([-1, -1, 1, -1, 1, -1, -1, -1, 1])

logistic_loss(y_true, y_pred).mean()

0.535483909740445

Exponential Loss

\begin{align} L(h_w(x_i), y_i) = e^{-h_w(x_i) y_i} \end{align}

• Adaboost

• Very aggressive, Loss of misprediction increases exponentially

def exp_loss(y_true, y_pred):
    return np.exp(-(y_pred * y_true))

Correct classification

exp_loss(-1, -1), exp_loss(1, 1)

(0.36787944117144233, 0.36787944117144233)

Incorrect Classification

exp_loss(-1, 1), exp_loss(1, -1)

(2.718281828459045, 2.718281828459045)

y_true = np.array([1, -1, 1, -1, 1, -1, 1, -1, 1])
y_pred = np.array([-1, -1, 1, -1, 1, -1, -1, -1, 1])

exp_loss(y_true, y_pred).mean()

0.8901910827909096

Zero-One Loss

\begin{align} L(h_w(x_i), y_i) &= \delta(sign({h_w(x_i)) \ne y_i}) \\ \\ \delta &= \begin{cases} 1 & \text{if } sign(h_w(x_i)) \ne y_i \text{ i.e. missclassification}\\ \\ 0 & \text{otherwise} \end{cases} \end{align}

• Actual Classification loss

def zero_one_loss(y_true, y_pred):
    return np.int32(np.sign(y_pred) != y_true)

Correct classification

zero_one_loss(-1, -1), zero_one_loss(1, 1)

(0, 0)

Incorrect Classification

zero_one_loss(-1, 1), zero_one_loss(-1, 1)

(1, 1)

y_true = np.array([1, -1, 1, -1, 1, -1, 1, -1, 1])
y_pred = np.array([-1, -1, 1, -1, 1, -1, -1, -1, 1])

zero_one_loss(y_true, y_pred).mean()

0.2222222222222222

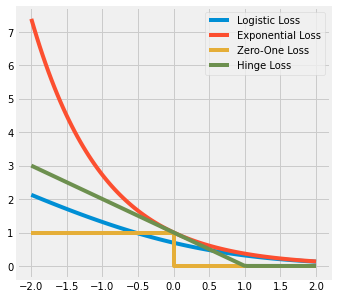
Graphical Representation

n_samples = 100

x = np.linspace(-2, 2, n_samples)
y = np.ones_like(x)

fig, ax = plt.subplots(1, 1, figsize=(5, 5))

ax.plot(x, logistic_loss(x, y), label='Logistic Loss')
ax.plot(x, exp_loss(x, y), label='Exponential Loss')
ax.plot(np.int32(x), zero_one_loss(y, x), label='Zero-One Loss')
ax.plot(x, hinge_loss(x, y, 1), label='Hinge Loss')

plt.legend()
plt.show()

Regression Loss

Squared Loss

\begin{align} L(h_w(x_i), y_i) &= (h_w(x_i) - y_i)^2 \end{align}

• also known as Ordinary Least Square

• estimates mean label

• Differenciable easily

• affected by noisy data

def squared_loss(y_true, y_pred):
    return np.square(y_pred - y_true)

y_true = np.array([12, 11, 10, 12.3, 11.2, 10.3])
y_pred = np.array([11.9, 11, 9.6, 12, 11, 10.1])

squared_loss(y_true, y_pred).mean(), metrics.mean_squared_error(y_true, y_pred)

(0.05666666666666679, 0.05666666666666679)

Absolute Loss

\begin{align} L(h_w(x_i), y_i) &= |h_w(x_i) - y_i| \end{align}

• Estimates median label

• Less sensitive to noise

def absolute_loss(y_true, y_pred):
    return np.abs(y_pred - y_true)

y_true = np.array([12, 11, 10, 12.3, 11.2, 10.3])
y_pred = np.array([11.9, 11, 9.6, 12, 11, 10.1])

absolute_loss(y_true, y_pred).mean(), metrics.mean_absolute_error(y_true, y_pred)

(0.20000000000000018, 0.20000000000000018)

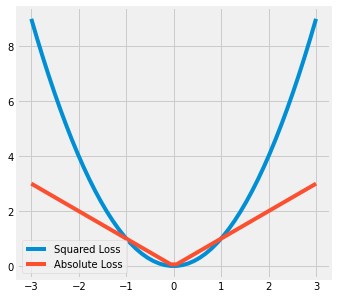
Graphical Representation

n_samples = 50

x = np.linspace(-3, 3, n_samples)
y = np.zeros_like(x)

fig, ax = plt.subplots(1, 1, figsize=(5, 5))

ax.plot(x, squared_loss(x, y), label='Squared Loss')
ax.plot(x, absolute_loss(x, y), label='Absolute Loss')

plt.legend()
plt.show()